非绝热动力学在化学以及生物、能源以及材料等交叉领域中的很多关键分子过程中至关重要。比如新型有机太阳能电池中激子单重态裂变过程、电动汽车动力电池中电子耦合锂离子扩散过程。实现复杂体系原子尺度上精确有效的非绝热动力学模拟可以为理解相关过程的微观机理、构建分子模型提供直接有力的帮助，从而为设计开发新能源材料，突破产业技术瓶颈铺平道路。

      非绝热动力学过程中涉及不同势能面之间的（无辐射）跃迁，电子与原子核的运动因为核-电子耦合作用无法有效分离，从而导致波恩-奥本海默近似（即绝热近似）失效。实现精确有效的非绝热动力学模拟要求理论方法能够自洽统一地处理原子核和电子耦合的量子动力学，因而对于复杂体系的模拟运算成本非常昂贵，是目前学术界亟待解决的难题。

      尽管用于研究非绝热动力学的理论方法很多，能够有效模拟复杂分子体系的非绝热动力学方法凤毛麟角。目前应用最为广泛的主要有平均场（Ehrenfest, EF）和势能面迁越（surface hopping, SH）方法，但是由于方法本身的不自洽性（对于电子和原子核分别采用量子、经典方法处理），它们都无法准确描述非绝热动力学中的量子效应（比如量子相干），有时会给出不合理的结果。

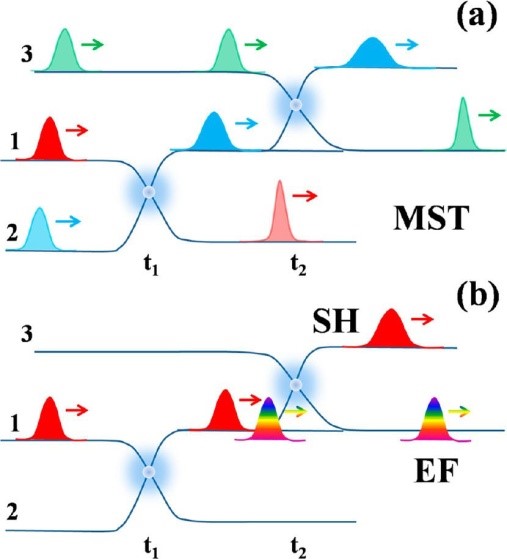
      为了实现实际体系非绝热分子动力学的精确有效模拟，在前期工作的基础上[J. Phys. Chem. Lett. 2010, 1, 891; Mol. Phys. 2013, 111, 1987; J. Phys. Chem. A 2013, 117, 5821; J. Phys. Chem. C 2014, 118, 17299; 2014, 118, 27258; and J. Chem. Theo. Comput. 2015, 11, 28], 陶国华副教授最近开发了一种多态轨线方法 [MST, J. Chem. Phys. 2016, 144, 094108]。该方法基于Meyer-Miller 电子态经典映射理论，提出描述原子核-电子耦合体系的多态轨线表示，即每个电子态由相应的运动轨线描述，而整个体系的动力学过程由所有电子态对应轨线的集合来描述，体系在特定时间所处的电子态由对称准经典窗口函数确定。多态轨线方法为理解量子动力学提供了全新的半经典诠释，物理图像清晰，对于每个电子态特定的动力学描述更准确（见图示1），核-电子耦合处理自洽，方法经济有效，具有优异的数值稳定性和实用性。新方法对于非绝热动力学过程具有普遍适用性，目前在处理实际的复杂材料体系的动力学过程已取得初步成果[J. Phys. Chem. C 2016]。

      该工作得到北京大学深圳研究生院，深圳市科技创新委，国家自然科学基金委的资助。
                        


文章链接：http://dx.doi.org/10.1063/1.4943006
Guohua Tao, “A multi-state trajectory method for non-adiabatic dynamics simulations”, The Journal of Chemical Physics 2016, 144 (9), 094108.